Sutton RL - Ch1. Multi-armed Bandits (2)
Posted on
-Greedy Action Selection
greedy action selection을 진행할 경우, 항상 exploiting만 진행합니다.
따라서, 학습을 진행함에 따라 가 에 가까워지지 않게 되어 장기적으로 좋지 못한 퍼포먼스를 보이게 됩니다.
-greedy action selection는 greedy action selection을 기본으로 하나, 의 확률로 greedy한 action 대신에 random action을 취하는 방법입니다.
이 때, random하게 선택되는 actions set에는 greedy action도 포함됩니다.
-greedy action selection의 알고리즘은 다음과 같습니다.
Initialize, for a=1 to k:
Q(a) <- 0
N(a) <- 0
Repeat forever:
A <- {a which maximizes Q(a), with probability (1 - epsilon)} or
{a random action, with probability epsilon}
R <- bandit(A)
N(A) <- N(A) + 1
Q(A) <- Q(A) + {1 / N(A)} [R - Q(A)]
-greedy의 10-armed testbed에서의 시행결과는 아래 그래프와 같습니다.
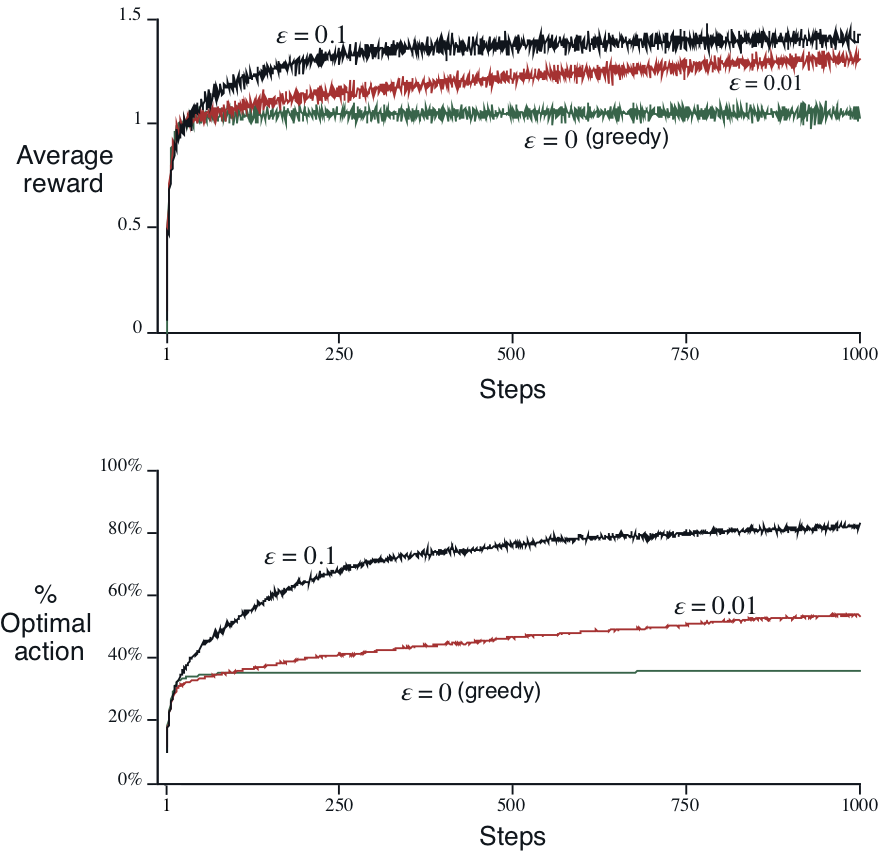
값을 어떻게 선택하느냐에 따라서 의 로의 수렴속도와 average reward의 수렴값이 다르게 됩니다.
상대적으로 큰 값을 선택할 경우, 빠른 속도로 action value estimiation의 수렴이 발생하여(학습이 빠르게 진행되어) optimal action을 취할 수 있게 되지만, 수렴이 발생한 뒤에도 지속적으로 random한 action을 선택하기 때문에, 최종 average reward 수렴값의 한계가 낮습니다.
상대적으로 작은 값을 선택할 경우, action value estimation의 수렴이 느리게 진행되어(학습이 천천히 진행되어) optimal action을 알게 되는 지점이 상대적으로 늦어 average reward가 상대적으로 천천히 증가하지만, 수렴이 발생한 뒤에는 random action을 선택하는 비율이 작기 때문에, 최종 average reward 수렴값의 한계가 높습니다.
을 전체 action중 exploring의 비율이라고도 생각할 수 있습니다.
-greedy는 간단하지만 값에 따라 수렴속도와 최종성능간의 trade-off관계가 있습니다.
이는 exploration / exploitation dilemma에서 이 비율을 고정적으로 가져갔기 때문입니다.
학습 초기에는 exploring의 비중을 크게, 학습이 진행되어 가 에 가까워짐에 따라 exploiting의 비중을 크게 변경하는 방식으로 adaptive하게 비율을 조정할 경우, 이러한 trade-off관계로부터 자유로워질 수 있을 것이라 판단할 수 있습니다.
이후 소개하는 방법들은 모두 이런 아이디어로부터 도출된 방법들입니다.
Optimistic Initial Values
exploration / exploitation 비율을 가변적으로 가져가는 방법들 중, 먼저 initial value를 편향시켜 학습을 진행하는 방법에 대하여 보겠습니다.
지금까지는 로 학습을 진행하였지만, 이번에는 대신에 큰 값을 대입하여 학습을 진행합니다.
10-armed testbed에서 로 학습한 결과는 아래 그래프와 같습니다.
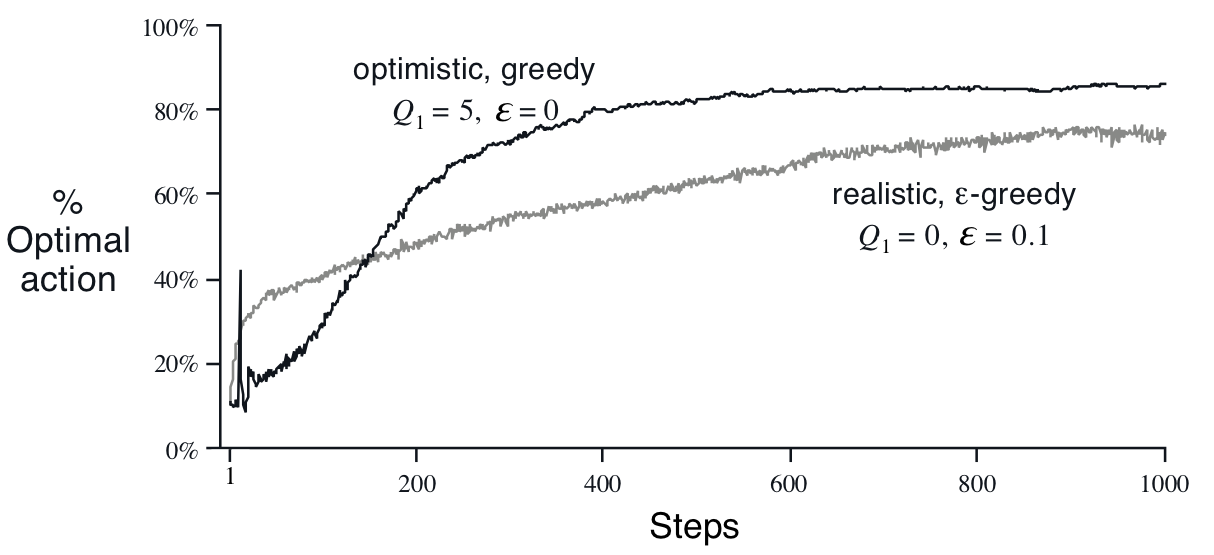
에서, 이 값은 10-armed testbed의 true action values보다 높은 값입니다. 따라서, incremental update를 진행할 때, 변분치 값이 음수가 되고, 가 작아지게 됩니다.
이처럼 초기 값을 높게 잡아 가 작아지는 방향으로 학습을 진행할 경우, 이전에 선택되어 가 업데이트된 action은 다른 action들보다 value값이 작아지게 되고, 때문에 다음 step에서 greedy한 선택을 할 경우 다른 action이 선택될 가능성이 높습니다.
예를 들어, action 이 1을, 가 2를, 이 3의 고정값을 반환하는 문제로 간단하게 하여 생각해 볼 경우 다음과 같은 과정을 거치게 됩니다.
서술 편의상 의 밑을 time step t가 아닌, 해당 action을 시행한 횟수 n으로 합니다.
step 1: , ,
- (greedy selection) 값이 모두 동일하므로 랜덤하게 선택, 리턴
- (의 밑이 가 아니라, 임에 주의)
step 2: , ,
- (greedy selection) 이므로 둘 중 랜덤하게 선택, 리턴
step 3: , ,
- (greedy selection) 이 가장 크므로 선택, 리턴
step 4: , ,
- (greedy selection) 이 가장 크므로 선택, 리턴
- …
고정값을 반환하는 문제로 간단하게 문제를 변형시켰기에 에서 바로 가 수렴하였지만, 실제 문제에서는 정규분포에 따라 임의의 값을 reward로 리턴받기 때문에 큰 time step까지 반복적 수행을 통하여 를 에 가깝게 수렴시킬 필요가 있습니다.
수행 과정을 보면, 이전에 수행하여 값이 작아진 action은 다음 step에서 선택될 가능성이 낮은 것을 확인할 수 있습니다. 를 작게 설정하여, 값이 커지는 방향으로 greedy 학습을 진행할 경우, greedy selection 단계에서 이전에 수행하여 가 커진 action을 다시 선택하게 되므로 exploring이 발생하지 않게 되는 것과 대조적입니다.
비교를 위하여, 같은 문제를 의 greedy selection으로 수행하는 과정을 나타내었습니다.
step 1: , ,
- (greedy selection) 값이 모두 동일하므로 랜덤하게 선택, 리턴
step 2: , ,
- (greedy selection) 이 가장 크므로 선택, 리턴
step 3: , ,
- (greedy selection) 이 가장 크므로 선택, 리턴
- …
exploring이 전혀 발생하지 않는 것을 확인할 수 있습니다.
Mysterious Spikes
optimistic initial values를 10-armed testbed에 적용한 위 그래프에서, 학습 초기단계에 optimal action을 거의 찾아내지 못하다가(10%) optimal action을 40% 확률로 찾아내는 spike가 있습니다. 이 spike는 에서 발생하며, 에서는 optimal action을 찾을 확률이 다시 급격하게 감소합니다. 해당 그래프는 2000회씩 반복된 시행의 평균을 통한 그래프이기에 이러한 경향은 outlier가 아니며, 명확한 원인이 있는 현상입니다.
직접 10-armed testbed에 대하여 시행시키는 과정을 생각해 보면 이러한 경향성에 대한 이유를 찾을 수 있습니다.
optimistic initial values를 바르게 적용할 경우, 초기단계에서는 exploiting을 하지 않습니다. 모든 action들을 한번씩 시행하기 전까지는 한 번 시행했던 action은 다시 시행하지 않는 exploring만 진행합니다. 때문에 10-armed testbed에서는 이 기간()동안 일반적으로 10%의 퍼포먼스만 보여주게 됩니다. (확률적으로 주어지는 reward가 initial value보다 크게 주어져서 incremental update가 양의 방향으로 발생한 경우에는 이 구간 내일지라도 exploiting이 발생하나, 이는 일종의 사고 혹은 initial value의 설계미스이기 때문에 일반적인 경우로 볼 수 없습니다)
에서는, ()동안 업데이트한 를 바탕으로 greedy action selection을 진행합니다. 10개의 action을 한번씩 모두 취하여 데이터를 확보한 뒤, 이를 토대로 최초의 exploiting을 하니, 자연스럽게 optimal action을 선택할 확률이 치솟게 됩니다.
에서는 에서 얻은 정보를 바탕으로 가장 가 높은 action부터 순차적으로 선택, 배제하는 시행이 이루어지며 이 과정에서 exploring을 진행할 확률이 높습니다. 때문에 optimal action을 선택할 확률이 급격하게 떨어지게 됩니다.
이러한 이유로 에서 spike가 발생합니다.